How do you replace the batteries of a digital caliper?
How to replace batteries in a digital caliper |
||||
 |
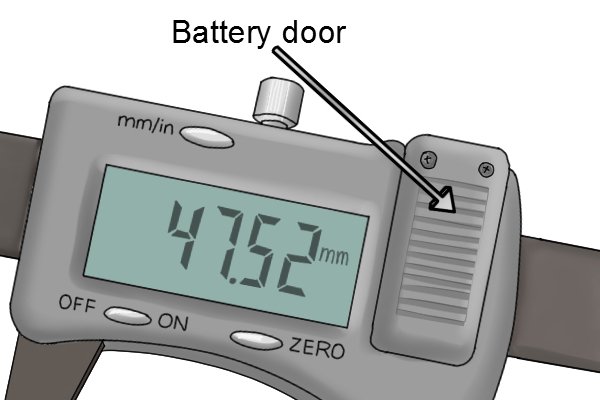The battery in a digital caliper can usually be found behind a battery door on the front of the tool. | |||
 |
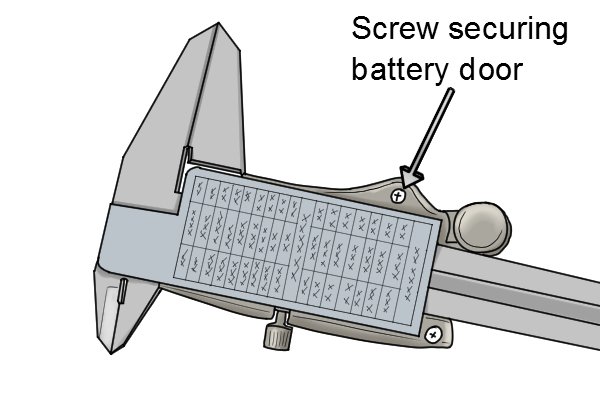Some calipers require the use of a screw driver.
The battery door is secured in place by a screw on the back of the caliper, which needs to be loosened. |
|||
 |
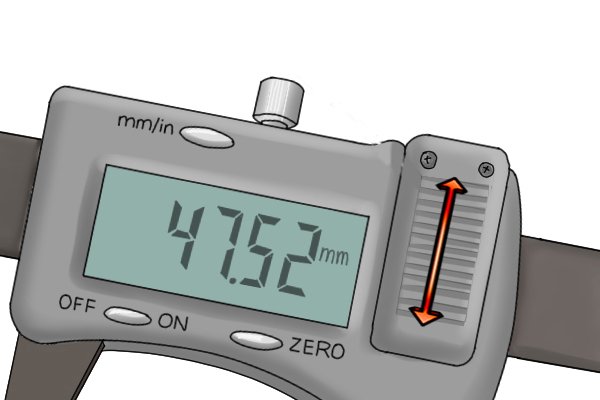The battery in other calipers can be accessed by sliding the battery door either upwards or downwards (depending on the caliper) until it clicks out of place. | |||
 |
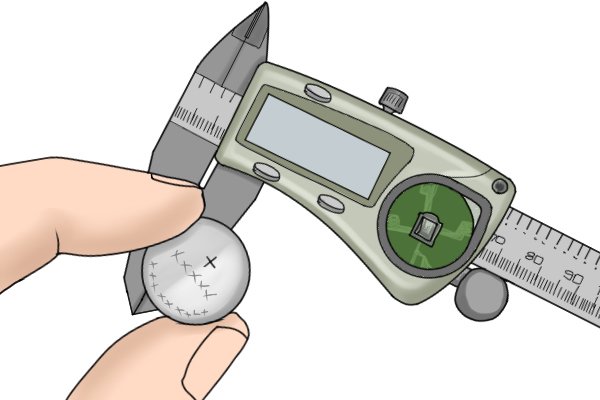After you have removed the old battery, replace it with a new one with the positive side up.
Then snap the cover back into place or secure it by replacing the screw you removed previously. |
|||
